【PyTorch】簡単なニューラルネットワークによる回帰分析を実装

今回はディープラーニング用ライブラリのPyTorchを利用し、ニューラルネットワークのモデルを構築して回帰分析を行う方法について書きます。

本記事における用語の説明

まずはいくつか用語の説明をします。

既に知っているという方は読み飛ばして下さい。

回帰分析とは

対象のデータから特定の数値を予測するための統計的手法のことです。

例としては、株価の予測（金利や為替などの情報から株価を予測）などが挙げられます。

ニューラルネットワークとは

AI関連技術である機械学習の代表的な手法の一つです。

基本単位のニューロンがいくつも連結することでネットワークを構築し、これを利用して様々な予測を行います。

ニューラルネットワークの内部は、一番最初にデータが入力される入力層、計算結果を出力する出力層、入力層と出力層の間の隠れ層のどれかに分類されます。

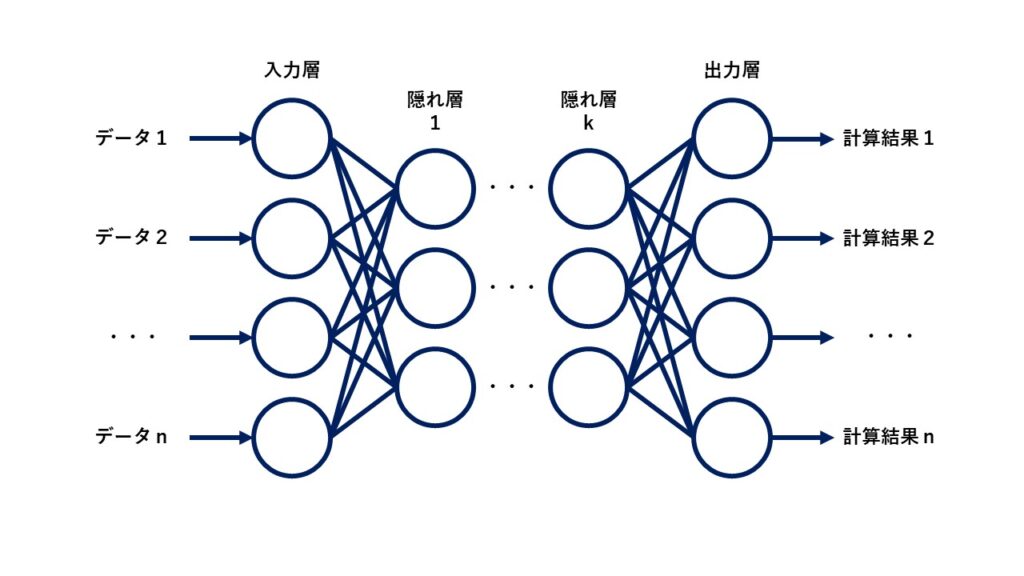
各層では入力された値を基に計算を行い、その計算結果を次の層のニューロンへ入力するという流れを入力層から出力層まで繰り返します。

各ニューロンにはどの入力を重要視するかを決定する重みがそれぞれ設定されており、重みの値を調整することで望ましい出力を得ることが可能です。

なお、ニューラルネットワークのメリット、デメリットはそれぞれ以下のようになります。

実際にプログラムを作成してみる

それでは、実際にニューラルネットワークのモデルを構築して回帰分析を行うプログラムを作成してみます。

プログラム作成の手順

ここでは、以下の手順で処理を実装します。

今回に限らず機械学習のモデルを構築する際には上記のような手順で実行することが多いです。

使用する実験用データセット

機械学習モデルの実験を行うには、当然、モデルに入力するデータが必要です。

今回は簡単なデータセットを自作して利用します。

作成するのは、以下のような分布のデータです。

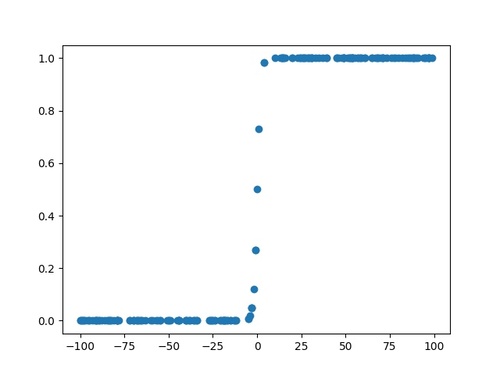
具体的なデータの作り方については、後ほど紹介するサンプルプログラムを参照して下さい。

モデルのハイパーパラメータ設定

今回はニューラルネットワークの分類モデルを以下の条件で構築します。

• 隠れ層の数：2
  　↳　ニューロンの数：(5, 5, )
• 活性化関数：
  　↳　出力層以外：ReLU関数
  　↳　出力層　　：恒等関数（活性化関数は適用せず）
• 最適化アルゴリズム：SGD
• 損失関数：平均二乗誤差関数

具体的な実装方法については、後ほど紹介するサンプルプログラムを参照して下さい。

実装例

上記の手順に従ってプログラムを作成します。使用する言語はPythonです。

import torch

# ニューラルネットワークの回帰モデルのクラス
class NNRegressor(torch.nn.Module):

    # コンストラクタ
    def __init__(self, input_size, output_size):
        super(NNRegressor, self).__init__()
        self.fc1 = torch.nn.Linear(input_size, 5)
        self.fc2 = torch.nn.Linear(5, 5)
        self.fc3 = torch.nn.Linear(5, output_size)

    # 順伝播の計算を行うメソッド
    def forward(self, x):
        y = torch.nn.functional.relu(self.fc1(x))
        y = torch.nn.functional.relu(self.fc2(y))
        y = self.fc3(y)
        return y

if __name__ == '__main__':

    train_size = 100
    test_size = 100
    data_size = train_size + test_size

    # 実験用データセットを作成
    x = torch.randint(-100, 100, (data_size, 1))
    t = 1 / (1 + torch.exp(-x + 1.0e-8))

    perm = torch.randperm(data_size)

    # データセットを学習用とテスト用に分割
    i_train, i_test = perm[:train_size], perm[train_size:]
    x_train, x_test = x[i_train].float(), x[i_test].float()
    t_train, t_test = t[i_train].float(), t[i_test].float()

    input_size = x.size()[1]
    output_size = t.size()[1]

    nnr = NNRegressor(input_size, output_size)
    nnr.train()

    lr = 0.01
    n_epochs = 20

    # 最適化アルゴリズムと損失関数を定義
    optimizer = torch.optim.SGD(nnr.parameters(), lr=lr)
    criterion = torch.nn.MSELoss()

    # モデルの学習を実施
    for epoch in range(n_epochs):
        for x, t in zip(x_train, t_train):
            nnr.zero_grad()
            y = nnr(x)
            loss = criterion(t, y)
            loss.backward()
            optimizer.step()
        print('( Train ) Epoch : %.2d, Loss : %f' % (epoch + 1, loss))

    # モデルのテストを実施
    print('-------------------------------------')
    y_test = nnr(x_test)
    score = torch.mean((t_test - y_test) ** 2)
    print('( Test )  MSE Score : %f' % score)

このプログラムを実行すると以下の出力結果が得られます。

( Train ) Epoch : 01, Loss : 0.061482
( Train ) Epoch : 02, Loss : 0.010420
( Train ) Epoch : 03, Loss : 0.001836
( Train ) Epoch : 04, Loss : 0.000355
( Train ) Epoch : 05, Loss : 0.000083
( Train ) Epoch : 06, Loss : 0.000027
( Train ) Epoch : 07, Loss : 0.000013
( Train ) Epoch : 08, Loss : 0.000009
( Train ) Epoch : 09, Loss : 0.000008
( Train ) Epoch : 10, Loss : 0.000008
( Train ) Epoch : 11, Loss : 0.000008
( Train ) Epoch : 12, Loss : 0.000008
( Train ) Epoch : 13, Loss : 0.000008
( Train ) Epoch : 14, Loss : 0.000008
( Train ) Epoch : 15, Loss : 0.000008
( Train ) Epoch : 16, Loss : 0.000008
( Train ) Epoch : 17, Loss : 0.000008
( Train ) Epoch : 18, Loss : 0.000008
( Train ) Epoch : 19, Loss : 0.000009
( Train ) Epoch : 20, Loss : 0.000009
-------------------------------------
( Test )  MSE Score : 0.003565

学習を通して損失関数の値が減少し、テストでも平均二乗誤差が0.003となっています。

このことから十分な性能のニューラルネットワークの回帰モデルを構築できたと考えられます。