本記事では、機械学習ライブラリのscikit-learnを利用し、ランダムフォレストのアルゴリズムに基づいて回帰分析を行う方法について書きます。
本記事における用語の説明

まずはいくつか用語の説明をします。
既に知っているという方は読み飛ばして下さい。
回帰分析とは
対象のデータから特定の数値を予測するための統計的手法のことです。
例としては、株価の予測(金利や為替などの情報から株価を予測)などが挙げられます。
ランダムフォレストとは
AI関連技術である機械学習の代表的な手法の一つです。同じく機械学習手法の決定木をベースとしています。決定木についての解説は以下の記事を参照して下さい。
【scikit-learn】決定木による回帰分析【DecisionTreeRegressor】
ランダムフォレストでは、複数の決定木モデルを生成し、それらモデルの多数決によって最終的な予測を決定するという仕組みです。
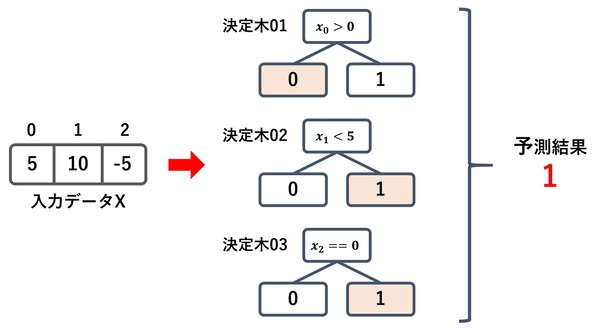
各モデルは元々の学習用データセットを分割して生成したサブデータセットを用いて学習を行うため、それぞれが微妙に異なる予測性能を発揮します。
そのため、生成する決定木モデルの数が多いほど、ランダムフォレスト全体としての汎化能力が高まり、予測の性能も向上する傾向があります。
なお、ランダムフォレストのメリット、デメリットはそれぞれ以下の通りです。
- メリット:
入力データに含まれる各特徴量の重要度の算出が可能 - デメリット:
複数の決定木モデルを使用するため、計算時間が長くなりやすい
実際にプログラムを作成してみる

ランダムフォレストのアルゴリズムに基づいて回帰分析を行うプログラムを作成してみます。
プログラム作成の手順
ここでは、以下の手順で処理を実装します。
- 実験用のデータセットを用意する
- データセットの一部を利用して学習(モデルの構築)を行う
- 構築したモデルを用いて残りのデータセットに対する予測を行う
今回に限らず、機械学習のモデルを構築する際には上記手順で実行することが多いです。
使用する実験用データセット
scikit-learnには、学習やテストで使用する実験用のデータセットが用意されているため、今回はその中の一つのボストンの住宅価格データ(load_boston)を使用します。
使用するデータセットの概要は以下の通りです。
- 用途:回帰
- データ件数:506
- データ次元数:13
- ドキュメント:sklearn.datasets.load_boston
ボストン市内の地域ごとの犯罪率や税率などの情報(13項目)を入力データとしてその地域の住宅価格を予測します。
モデル構築に使用するクラス
scikit-learnには、ランダムフォレストのアルゴリズムに基づいて回帰分析の処理を行うRandomForestRegressorクラスが存在するため、今回はこれを利用します。
RandomForestRegressorの主なパラメータは以下の通りです。(一部省略)
- n_estimators:int型
使用する決定木の数 - criterion:{‘mse’, ‘mae’}
学習時、モデルの評価に使用する指標 - max_depth:int型 or None
決定木の深さの最大値(Noneの場合は、深さの制限無し) - random_state:int型
乱数のシードを指定する
RandomForestRegressorはsklearn.ensembleパッケージからインポートします。
実装例
上記の手順に従ってプログラムを作成します。使用する言語はPythonです。
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
import random
if __name__ == '__main__':
# データセットを読み込む
boston = load_boston()
x = boston.data
y = boston.target
# 読み込んだデータセットをシャッフルする
p = list(zip(x, y))
random.shuffle(p)
x, y = zip(*p)
# 学習データの件数を指定する
train_size = 300
test_size = len(x) - train_size
# データセットを学習データとテストデータに分割する
train_x = x[:train_size]
train_y = y[:train_size]
test_x = x[train_size:]
test_y = y[train_size:]
# ランダムフォレストの学習を行う
rfr = RandomForestRegressor(n_estimators=100, criterion='mse', max_depth=None)
rfr.fit(train_x, train_y)
# 学習させたモデルを使ってテストデータに対する予測を出力する
pred = rfr.predict(test_x)
for i in range(test_size):
c = test_y[i]
p = pred[i]
print('[{0}] correct:{1:.3f}, predict:{2:.3f} ({3:.3f})'.format(i, c, p, c-p))
# 予測結果から決定係数を算出する
print('R^2 = {0}'.format(rfr.score(test_x, test_y)))このプログラムを実行すると以下の出力結果が得られます。
[0] correct:31.000, predict:30.511 (0.489) [1] correct:27.500, predict:28.919 (-1.419) [2] correct:23.000, predict:24.352 (-1.352) ...省略... [203] correct:22.100, predict:24.609 (-2.509) [204] correct:50.000, predict:48.033 (1.967) [205] correct:8.300, predict:10.208 (-1.908) R^2 = 0.8562013016638912
出力結果の最後の行は「決定係数」の値です。
決定係数とは、回帰分析において正解の値と予測値の誤差を算出した指標であり、その値が1.0に近いほど良い予測性能であると評価されます。
一般的に決定係数が0.6以上あれば予測モデルとして一定の性能を持つとされているため、上記のプログラムで構築したモデルは十分な予測性能であると判断できます。



