【scikit-learn】決定境界の可視化

機械学習の手法を用いたクラス分類において、各分類モデルの決定境界を可視化して比較、考察することがしばしばあります。

この記事では、そのためのプログラム作成の方法などについて解説しています。

そもそも「決定境界」とは？

まずは決定境界とは何かについて簡単に説明します。

分類の基準となる境界線

決定境界とは、データの分類予測を行う際に予測の基準となる境界線のことです。

学習済のモデルが値域内の各点においてどのような分類予測を行うのかを調べることで決定境界を求めることができます。

以下の図は実際に決定境界を可視化したものです。

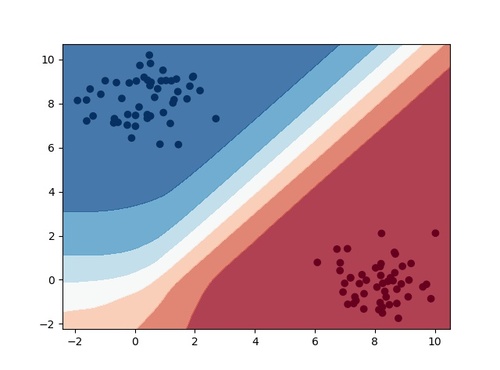
ちなみに上の図はとあるサンプルデータを学習させたニューラルネットワークの決定境界ですが、機械学習手法によって出来上がる決定境界は異なります。

決定境界の形を比較することで対象の分類問題にどの機械学習手法を適用すればよいのかの判断に役立てることも可能です。

実際にプログラムを作成してみる

それでは実際に決定境界の可視化を行うプログラムを作成してみます。

プログラム作成の手順

ここでは、以下の手順で処理を実装します。

実装例

上記の手順に従ってプログラムを作成します。使用する言語はPythonです。

from sklearn.datasets import make_blobs
from sklearn.neural_network import MLPClassifier

import matplotlib.pyplot as plt
import numpy as np

if __name__ == "__main__":

    # サンプルデータを生成する
    x, y = make_blobs(n_samples=100, n_features=2, centers=2)

    # 分類モデル（※今回はニューラルネットワーク）を作成する
    estimator = MLPClassifier()
    estimator.fit(x, y)

    # サンプルデータの値域を求める
    f1_min = x[:, 0].min() - 0.5
    f1_max = x[:, 0].max() + 0.5
    f2_min = x[:, 1].min() - 0.5
    f2_max = x[:, 1].max() + 0.5

    step = 0.02
    f1_range = np.arange(f1_min, f1_max, step)
    f2_range = np.arange(f2_min, f2_max, step)
    f1, f2 = np.meshgrid(f1_range, f2_range)

    # 決定境界を描画する
    Z = estimator.predict_proba(np.c_[f1.ravel(), f2.ravel()])[:, 1]
    Z = Z.reshape(f1.shape)

    plt.contourf(f1, f2, Z, cmap=plt.cm.RdBu, alpha=0.8)
    plt.scatter(x[:,0], x[:,1], c=y, cmap=plt.cm.RdBu)
    plt.show()

このプログラムを実行すると以下の出力結果が得られます。

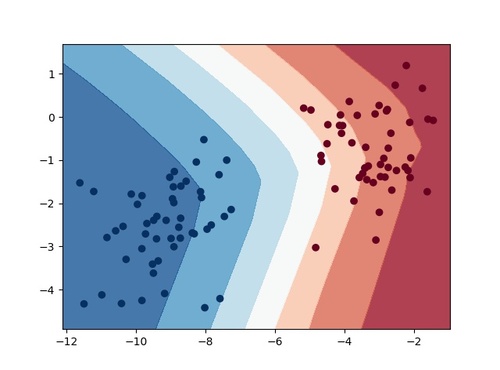
綺麗に決定境界を可視化することができました。ちなみに分類モデルはニューラルネットワークです。

応用：複数の決定境界の同時プロット

上記のプログラムでも決定境界の可視化は問題なく行えますが、複数のモデルの決定境界を同時に可視化することはできません。

最後に複数のデータやモデルについてそれぞれの決定境界を比較しやすいよう同時に可視化するプログラムの作成方法についても紹介しておきます。

実装例

同様の手順でプログラムを作成します。使用する言語はPythonです。

from sklearn.datasets import make_blobs, make_moons, make_circles
from sklearn.neural_network import MLPClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC

import matplotlib.pyplot as plt
import numpy as np

# 決定境界をプロットするメソッド
def plot_decision_boundary(ax, x, y, estimator, cmap=plt.cm.RdBu, step=0.02):
    f1_min = x[:, 0].min() - 0.5
    f1_max = x[:, 0].max() + 0.5
    f2_min = x[:, 1].min() - 0.5
    f2_max = x[:, 1].max() + 0.5
    f1_range = np.arange(f1_min, f1_max, step)
    f2_range = np.arange(f2_min, f2_max, step)
    f1, f2 = np.meshgrid(f1_range, f2_range)
    estimator.fit(x, y)
    if hasattr(estimator, "decision_function"):
        Z = estimator.decision_function(np.c_[f1.ravel(), f2.ravel()])
    else:
        Z = estimator.predict_proba(np.c_[f1.ravel(), f2.ravel()])[:, 1]
    Z = Z.reshape(f1.shape)
    ax.contourf(f1, f2, Z, cmap=cmap, alpha=0.8)

if __name__ == "__main__":

    # サンプルデータを生成する
    blobs_x, blobs_y = make_blobs(n_samples=100, n_features=2, centers=2)
    moons_x, moons_y = make_moons(n_samples=100, noise=0.1)
    circle_x, circle_y = make_circles(n_samples=100, factor=0.5, noise=0.1)

    x = np.array([blobs_x, moons_x, circle_x])
    y = np.array([blobs_y, moons_y, circle_y])

    # 使用するモデルを定義する
    ESTIMATORS = {
        'Neural Network' : MLPClassifier(),
        'Decision Tree' : DecisionTreeClassifier(),
        'SVM' : SVC()
    }

    names = ['Input Data'] + list(ESTIMATORS.keys())
    estimators = list(ESTIMATORS.values())

    cmap = plt.cm.RdBu
    n_cols = len(x)
    n_rows = len(names)

    # 各モデルの決定境界をそれぞれプロットする
    fig, axes = plt.subplots(n_cols, n_rows, figsize=(8,8))
    for i in range(n_cols):
        for j in range(n_rows):
            if i==0:
                axes[i,j].set_title(names[j], fontsize=10)
            if j!=0:
                plot_decision_boundary(axes[i,j], x[i], y[i], estimators[j-1])
            axes[i,j].scatter(x[i,:,0], x[i,:,1], c=y[i], cmap=cmap)
            axes[i,j].set_xticks(())
            axes[i,j].set_yticks(())
    plt.tight_layout()
    plt.show()

このプログラムを実行すると以下の出力結果が得られます。

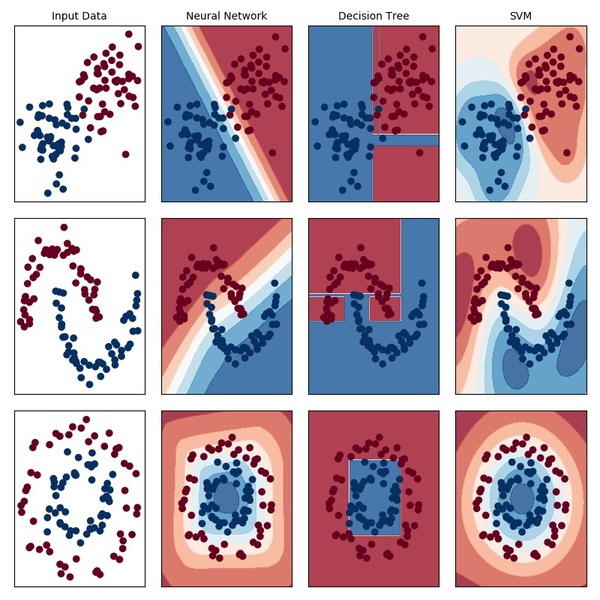
機械学習手法によって決定境界の出来にかなり違いがあることが一目でわかります。